[AcWing]3766. 二叉树的带权路径长度

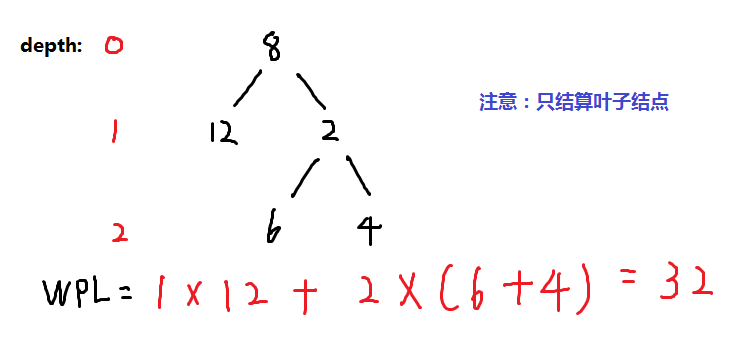
二叉树的带权路径长度(WPL)是二叉树中所有叶结点的带权路径长度之和，也就是每个叶结点的深度与权值之积的总和。

给定一棵二叉树 T，请你计算并输出它的 WPL。

注意，根节点的深度为 0。

样例

1
2
3
4
5
6
7
8
输入：二叉树[8, 12, 2, null, null, 6, 4, null, null, null, null]如下图所示：
    8
   / \
  12  2
     / \
    6   4

输出：32

数据范围

二叉树结点数量不超过 1000。
每个结点的权值均为不超过 100 的非负整数。

算法思想

从根结点到各叶结点的路径长度 * 相应叶节点权值 之和。

image-20240417204932311

代码实现1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int ans;

    void dfs(TreeNode * root, int depth){
        if(!root) return;
        
        // 只有叶子节点才承载有效的信息
        if(!root -> left && !root -> right){
            ans += depth * root -> val;
        }else{
            // 否则dfs
            dfs(root -> left, depth + 1);            
            dfs(root -> right, depth + 1);
        }
    }

    int pathSum(TreeNode* root) {
        dfs(root, 0);
        return ans;
    }
};

代码实现2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    int dfs(TreeNode * root, int depth){
        if(!root) return 0;
        
        // 只结算叶子结点的
        if(!root -> left && !root -> right) return depth * root -> val;
        
        return dfs(root -> left, depth + 1) + dfs(root -> right, depth + 1);
    }

    int pathSum(TreeNode* root) {
        return dfs(root, 0);
    }
};