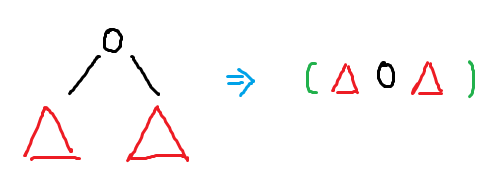[AcWing]3765. 表达式树

请设计一个算法，将给定的表达式树(二叉树)转换为等价的中缀表达式(通过括号反映操作符的计算次序)并输出。

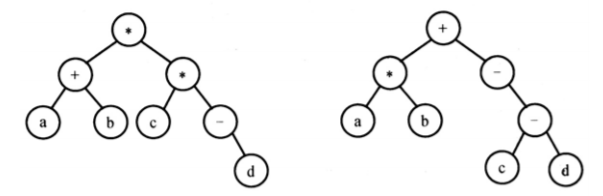
例如，当下列两棵表达式树作为算法的输入时：

QQ截图20210708095213.png

输出的等价中缀表达式分别为 (a+b)*(c*(-d)) 和 (a*b)+(-(c-d))。

注意：

  • 树中至少包含一个运算符。
  • 当运算符是负号时，左儿子为空，右儿子为需要取反的表达式。
  • 树中所有叶节点的值均为非负整数。

样例：

1
2
3
4
5
6
7
8
输入：二叉树[+, 12, *, null, null, 6, 4, null, null, null, null]如下图所示：
    +
   / \
  12  *
     / \
    6   4

输出：12+(6*4)

数据范围

给定二叉树的非空结点数量保证不超过 1000。

给定二叉树保证能够转化为合法的中缀表达式。

算法思想

很容易想到这是基于树的中序遍历的算法，难点在于加括号的时机。

通过观察发现，除了根节点，每棵子树都一直在重复做的事情：

image-20240404195438756

那么就会有

1
2
3
4
5
ans += "(";
dfs(root -> left);
ans += root -> val;
dfs(root -> right);
ans += ")";

在中序遍历之前需要加上括号。

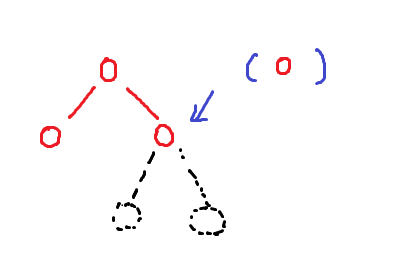
可是，有特殊情况：

image-20240404201019068

那么就需要特殊处理。

当碰到叶子结点的时候就不需要加括号了，直接输出结点值就行。
也就是说：只有叶子结点两边不加括号。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     string val；
 *     TreeNode *left;
 *     TreeNode *right;
 * };
 */
class Solution {
public:
    string ans;
    
    void dfs(TreeNode * root){
        if(!root) return;
        // 遇到叶子结点
        if(!root -> left && !root -> right){
            ans += root -> val;
        }else{
            // 非叶子结点
            ans += "(";
            dfs(root -> left);
            ans += root -> val;
            dfs(root -> right);
            ans += ")";
        }
    }

    string expressionTree(TreeNode * root) {
        // 处理根节点的特殊情况，直接处理左右子树
        dfs(root -> left);
        ans += root -> val;
        dfs(root -> right);
        
        return ans;
    }
};