[AcWing]49. 二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。

要求不能创建任何新的结点，只能调整树中结点指针的指向。

注意：

需要返回双向链表最左侧的节点。

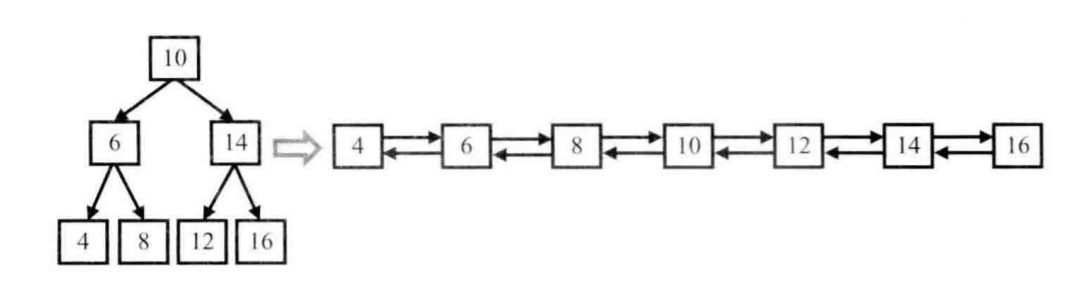
例如，输入下图中左边的二叉搜索树，则输出右边的排序双向链表。

QQ截图20181202052830.png

数据范围

树中节点数量 [0,500]。

算法思路

中序遍历的基本代码：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */

void dfs(TreeNode * cur){
    if(!cur) return;

    dfs(cur -> left);

    cout << cur -> val << " ";

    dfs(cur -> right);
}

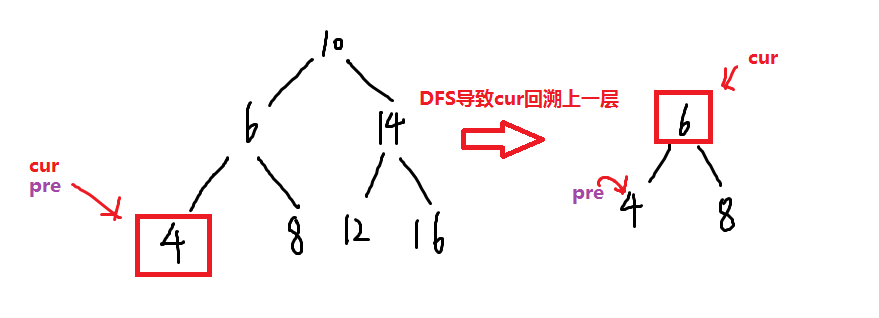
根据观察，考虑在二叉树的中序遍历的基础上，利用 pre 和 cur 来进行 双链表的构建。

先找到双链表的第一个节点，它是中序遍历的第一个节点。
定义一个指针cur，指向当前处理的节点。
如果cur的左子树不为空，则递归处理左子树。
将cur与其前驱节点（即中序遍历中cur的前一个节点）连接起来。
更新前驱节点为cur。
处理cur的右子树，重复步骤2-4。

代码实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    
    TreeNode * head, * pre;

    void dfs(TreeNode * cur){
        if(!cur) return;
        
        dfs(cur -> left);
        
        // 先找到中序遍历第一个节点作为双链表的head
        // 只有当dfs(cur -> left)压栈全部完毕才可能执行这行if，因此head一定是中序遍历的第一个元素
        if(!pre) head = cur;
        else{
            // 将cur与其前驱节点连接起来
            pre -> right = cur;
            // 构成双向
            cur -> left = pre;
        }
        
        // 将当前的节点变成下一次回溯的前驱节点
        pre = cur;
        
        dfs(cur -> right);
    }

    TreeNode* convert(TreeNode* root) {
        // 在中序遍历的基础上，做点改变 中序遍历：左根右
        dfs(root);
        return head;
    }
};