[AcWing]131. 直方图中最大的矩形

直方图是由在公共基线处对齐的一系列矩形组成的多边形。

矩形具有相等的宽度，但可以具有不同的高度。

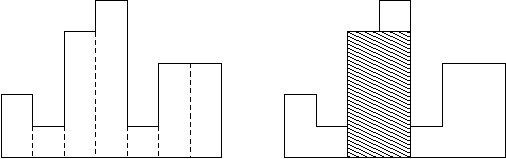
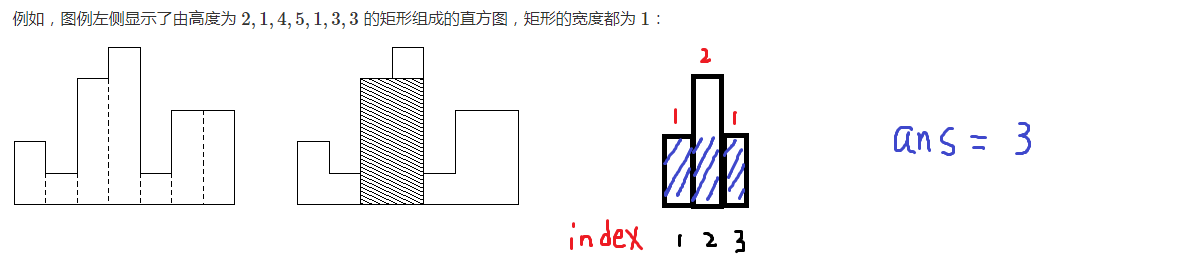
例如，图例左侧显示了由高度为 2,1,4,5,1,3,3 的矩形组成的直方图，矩形的宽度都为 1：

2559_1.jpg

通常，直方图用于表示离散分布，例如，文本中字符的频率。

现在，请你计算在公共基线处对齐的直方图中最大矩形的面积。

图例右图显示了所描绘直方图的最大对齐矩形。

输入格式

输入包含几个测试用例。

每个测试用例占据一行，用以描述一个直方图，并以整数 n 开始，表示组成直方图的矩形数目。

然后跟随 n 个整数 h_1，…，h_n。

这些数字以从左到右的顺序表示直方图的各个矩形的高度。

每个矩形的宽度为 1。

同行数字用空格隔开。

当输入用例为 n=0 时，结束输入，且该用例不用考虑。

输出格式

对于每一个测试用例，输出一个整数，代表指定直方图中最大矩形的区域面积。

每个数据占一行。

请注意，此矩形必须在公共基线处对齐。

数据范围

1 < n < 100000,
0 < h_i < 1000000000

输入样例：

1
2
3
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

输出样例：

1
2
8
4000

算法思想

对于每个矩阵，基于单调栈的算法，从左往右，从右往左，可以算出各自矩阵的最近且最小的矩阵位置是多少。

image-20240609203648376

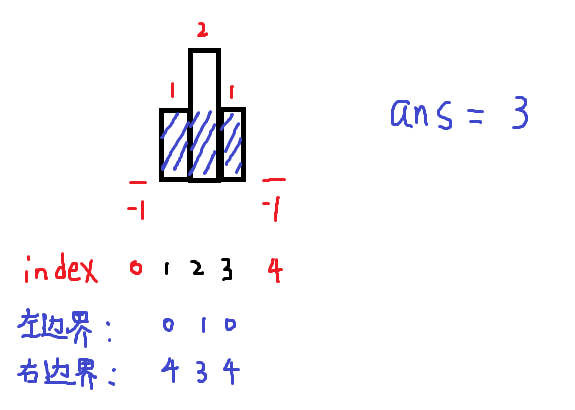
image-20240610214630320

边界预处理在这里的作用主要是为了避免在处理第一个和最后一个矩形时出现特殊情况。具体来说，当你从左到右遍历矩形并尝试找到它们的左边界时，对于第一个矩形（i=1），如果没有额外的预处理，你就没有办法找到一个左侧比它矮的矩形来确定其左边界，因为 h[0] 不存在。同样地，当你从右到左遍历矩形并尝试找到它们的右边界时，对于最后一个矩形（i=n），如果没有额外的预处理，你也没有办法找到一个右侧比它矮的矩形来确定其右边界，因为 h[n+1] 不存在。

具体来说：

当从左到右遍历时，对于第一个柱子 h[1]，如果没有 h[0] 作为哨兵，并且 h[1] 是所有柱子中最高的，那么 l[1] 将不会被正确设置（因为没有比它矮的柱子在左侧）。但是，由于我们设置了 h[0] = -1（一个比所有实际柱子都小的值），l[1] 就会被正确地设置为 0（或者说，没有柱子在 h[1] 的左侧）。
当从右到左遍历时，对于最后一个柱子 h[n]，如果没有 h[n+1] 作为哨兵，并且 h[n] 是所有柱子中最高的，那么 r[n] 将不会被正确设置（因为没有比它矮的柱子在右侧）。但是，由于我们设置了 h[n+1] = -1，r[n] 就会被正确地设置为 n+1（或者说，没有柱子在 h[n] 的右侧）。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#include <iostream>

using namespace std;

// 爆int
typedef long long ll;

const int N = 100010;

// h装每个矩形的高，l装每个矩形的左边界，r装每个矩形的右边界
// q是双端单调队列
int h[N], l[N], r[N], q[N];

int main(){
    
    int n;
    
    while(cin >> n, n){
        // 输入每个矩形的高
        for(int i = 1; i <= n; i++) cin >> h[i];
        
        // 让h[0]和h[n + 1]值为 -1，这样就不用处理边界问题了（什么边界问题？）
        h[0] = h[n + 1] = -1;
        
        int tt = 0;
        q[0] = 0;
        // 开始维护单调队列，从左往右
        for(int i = 1; i <= n; i++){
            // 维护
            while(tt && h[i] <= h[q[tt]]) tt--;
            // 左边界
            l[i] = q[tt];
            q[++tt] = i;
        }
        
        // 准备维护单调队列，从右往左
        tt = 0;
        q[0] = n + 1;
        
        for(int i = n; i ; i--){
            // 维护
            while(tt && h[i] <= h[q[tt]]) tt--;
            // 右边界
            r[i] = q[tt];
            q[++tt] = i;
        }
        
        ll res = 0;
        for(int i = 1; i <= n; i++){
            res = max(res, (ll)h[i] * (r[i] - l[i] - 1));
        }
        
        cout << res << endl;
    }
    
    return 0;
}