[AcWing. 154. 滑动窗口内求最大值和最小值]

给定一个大小为 n < 10^6 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

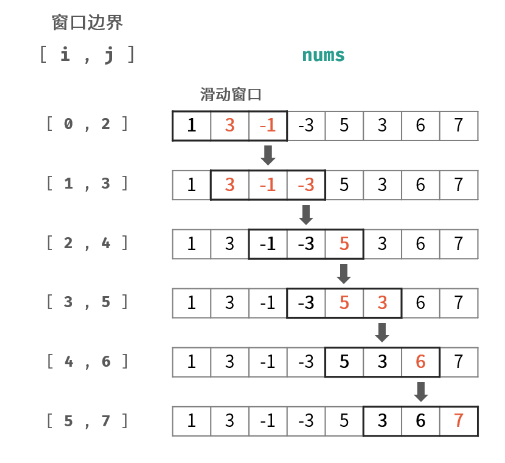
该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

窗口位置最小值最大值
[1 3 -1] -3 5 3 6 7-13
1 [3 -1 -3] 5 3 6 7-33
1 3 [-1 -3 5] 3 6 7-35
1 3 -1 [-3 5 3] 6 7-35
1 3 -1 -3 [5 3 6] 736
1 3 -1 -3 5 [3 6 7]37

你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

1
2
8 3
1 3 -1 -3 5 3 6 7

输出样例：

1
2
-1 -3 -3 -3 3 3
3 3 5 5 6 7

算法思想

滑动窗口，每次滑动一个单位，窗口内求最大最小值。

借图：

滑动窗口

题外话：在一个从小到大排列的数列中，若左边的数比右边的数大，就称作逆序数啊，如：1，3，5，4，6 中，5就是逆序数啊，看看5在题目中有没有用，若是没有用，那该题就有单调性。

  1. 使用双端单调队列：利用双端单调队列来高效维护滑动窗口的最小值和最大值。

  2. 维护窗口边界：在每次滑动时，检查队列头部的元素是否已经滑出窗口范围，如果是则移除。

  3. 保持单调性：
    对于最小值，保持队列单调递增，移除队列中比当前元素大的元素。
    对于最大值，保持队列单调递减，移除队列中比当前元素小的元素。
    插入新元素：将当前元素的索引插入队列。

  4. 输出结果：当窗口大小达到要求时，队首元素即为当前窗口的最小值或最大值。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>

using namespace std;

const int N = 1000010;

// 数组和双端单调队列
int a[N], q[N], hh = 0, tt = -1;
// 数组元素个数和滑动窗口的长度
int n, k;

int main() {
    cin >> n >> k;

    // 输入元素
    for (int i = 0; i < n; i++) cin >> a[i];

    // 求滑动窗口的最小值
    for (int i = 0; i < n; i++) {
        // 维护窗口，i - k + 1 是窗口的左边界
        // 如果队首元素的索引已经小于当前窗口的左边界
        // 说明该元素已经滑出窗口，需要将队首指针 hh 向后移动以排除这个元素
        if (hh <= tt && i - k + 1 > q[hh]) ++hh;
        
        // 保持队列单调递增，排除不可能的最小值
        while (hh <= tt && a[i] <= a[q[tt]]) --tt;
        
        // 当前元素入队
        q[++tt] = i;

        // 输出当前窗口的最小值
        if (i + 1 >= k) cout << a[q[hh]] << " ";
    }
    cout << endl;

    // 重置队列指针
    hh = 0;
    tt = -1;

    // 求滑动窗口的最大值
    for (int i = 0; i < n; i++) {
        // 维护窗口，i - k + 1 是窗口的左边界
        // 如果队首元素的索引已经小于当前窗口的左边界
        // 说明该元素已经滑出窗口，需要将队首指针 hh 向后移动以排除这个元素
        if (hh <= tt && i - k + 1 > q[hh]) ++hh;

        // 保持队列单调递减，排除不可能的最大值
        while (hh <= tt && a[i] >= a[q[tt]]) --tt;

        // 当前元素入队
        q[++tt] = i;

        // 输出当前窗口的最大值
        if (i + 1 >= k) cout << a[q[hh]] << " ";
    }

    return 0;
}