直接插入排序

本文将介绍基于数组的直接插入排序

算法的思想：维护一个有序序列，初始时有序序列只有一个元素即为第1个元素，随后选定数组的第2个元素为待插入元素 base ，将 base 与其左边的元素依次对比大小，并“插入”到正确位置。每次将一个新的元素插入到有序序列中，将有序序列的长度增加 1，直到全部元素都加入到有序序列中。

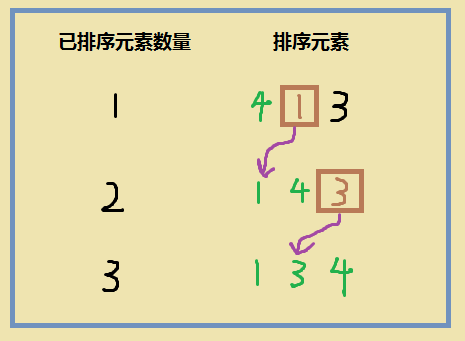
一个简单的例子：

算法流程

第1轮先选取排序元素中的第2个元素为base，base与它之前的所有元素一一比较，然后执行插入操作，至此元素中前2个元素已完成排序。
第2轮先选取排序元素中的第3个元素为base，base与它之前的所有元素一一比较，然后执行插入操作，至此元素中前3个元素已完成排序。

这样排序就完成了，有序序列长度从1变成了3，这个过程进行了2轮

算法特性

时间复杂度O(n²)：

最好情况：O(n)，比如：[1,2,3,4,5] 有序情况，整个过程未进行任何插入操作，仅进行比较操作
平均情况：O(n²)
最差情况：各轮插入操作循环n-1，n-2，…，2，1次，求和为 ((n - 1) x n ) / 2，使用O(n²)时间。

空间复杂度O(1)：变量 i , j 使用常数大小的额外空间。

稳定性：稳定（不交换相等元素）

直接插入排序 vs 冒泡排序

虽然「直接插入排序」和「冒泡排序」的时间复杂度皆为O(n²) ，但实际运行速度却有很大差别，这是为什么呢？

回顾复杂度分析，两个方法的循环次数都是((n - 1) x n )/2。但不同的是，「冒泡操作」是在做元素交换，需要借助一个临时变量实现，共 3 个单元操作；而「插入操作」是在做赋值，只需 1 个单元操作；因此，可以粗略估计出冒泡排序的计算开销约为直接插入排序的 3 倍。

// 冒泡排序的 元素交换
swap(q[j], q[j + 1]); // 这个函数实现一下就知道了 共3个单元操作
// 直接插入排序的 赋值
q[j + 1] = q[j];

直接插入排序运行速度快，并且具有原地（指针变量仅使用常数大小额外空间）、稳定（不交换相等元素）、自适应（最佳情况下，时间复杂度为O(n²)的优点，因此很受欢迎。实际上，包括 Java 在内的许多编程语言的排序库函数的实现都用到了直接插入排序。库函数的大致思路：

对于长数组，采用基于分治的排序算法，例如快速排序，时间复杂度为O(nlogn)
对于短数组，直接使用直接插入排序，时间复杂度为O(n²)

在数组较短时，复杂度中的常数项（即每轮中的单元操作数量）占主导作用，此时插入排序运行地更快。

算法模板

void insert_sort(){
    // 外层循环保证 n - 1 趟的同时
    // 还保证了选取 第2个 元素作为base
    for(int i = 1 ; i < n ; i++){
        int base = q[i] , j = i;
        // 如果 j 大于 0 并且 base 比 q[j - 1] 小
        while(j && base < q[j - 1]){
            q[j] = q[j - 1];
            j--;
        }
        q[j] = base;
    }
}