二路归并排序

本文将用图例介绍二路归并排序的过程，和经典的板子

算法思想

归并排序和快速排序类似，是基于分治的算法，具有两个主要阶段「划分」和「合并」。

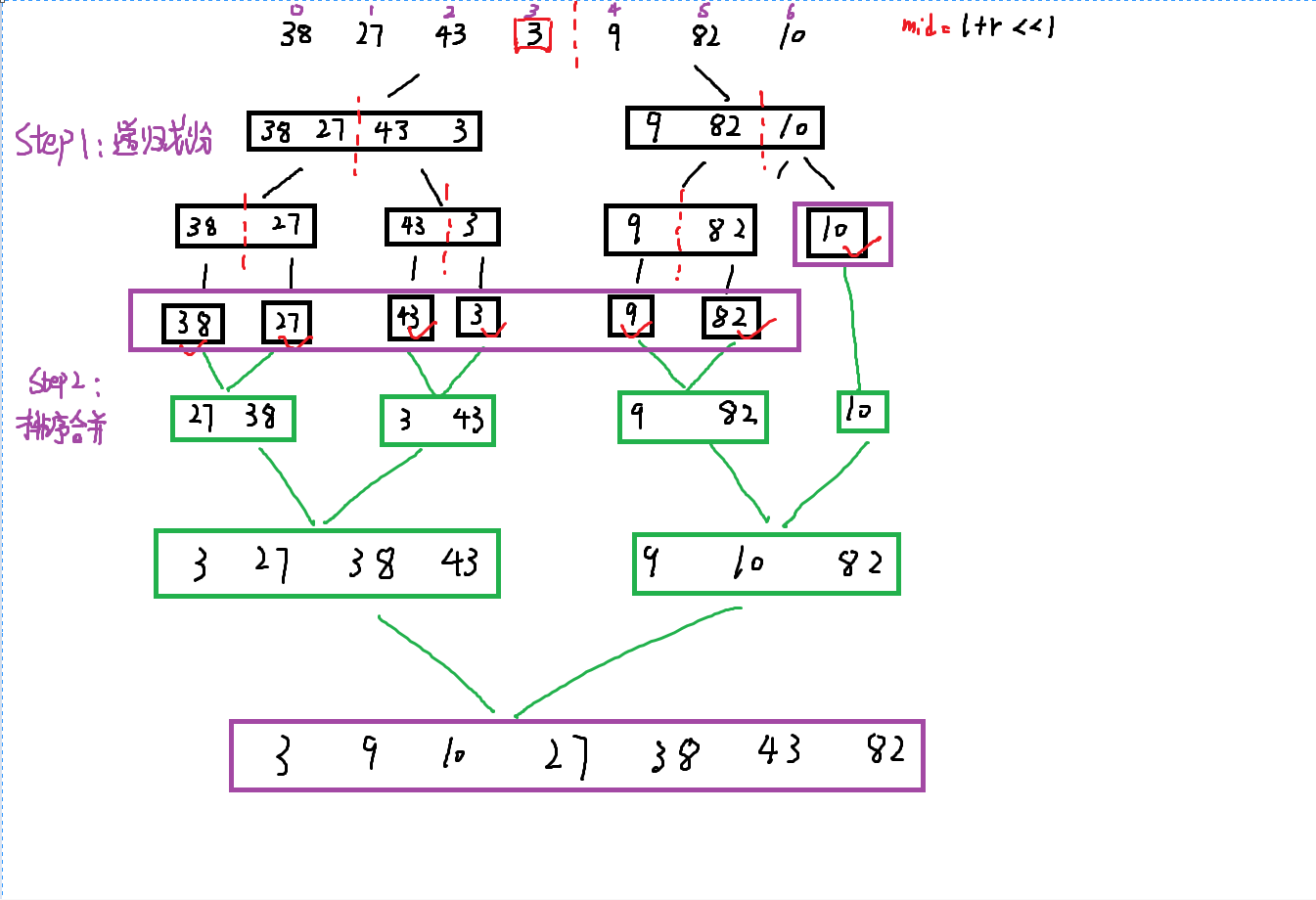
划分阶段：通过递归不断 将数组从中点位置划分开，将长数组的排序问题转化为短数组的排序问题；
合并阶段：划分到子数组长度为 1 时，开始向上合并，不断将 左、右两个短有序数组 合并为 一个长有序数组，直至合并至原数组时完成排序；

一个简单的例子：

2023-02-13_213202

算法特性

时间复杂度：「划分」阶段形成的递归树花费的时间为O(logn)，每层合并的总操作花费的时间为O(n)。因此总体时间复杂度为O(nlogn)
空间复杂度：它需要临时存储原始数据的副本，因此使用了 O(n) 的额外空间，排序过程需要借助一个额外的辅助数组O(n)大小，因此空间复杂度为O(n)。
提问：为什么归并排序的空间复杂度和递归深度无关？答：因为归并排序只需要复制原始数据的一份副本，而不需要将原始数据进行划分，这样就避免了递归深度的影响。
稳定性：稳定

算法模板

int n;
int q[N] , w[N];

void merge_sort(int l , int r){
    // 区间长度为1 则停止继续划分
    if(l >= r) return;
    // 分割中点
    int mid = l + r >> 1;
    // 递归划分
    merge_sort(l , mid) ; merge_sort(mid + 1 , r);
	// 排序合并
    int i = l , j = mid + 1 , k = 0;
    // 在区间[l,mid]和[mid + 1, r]内
    // 排序合并一部分
    while(i <= mid && j <= r){
        if(q[i] <= q[j]) w[k++] = q[i++];
        else w[k++] = q[j++];
    }
    // 剩下的有序数组直接填入辅助数组内
    while(i <= mid) w[k++] = q[i++];
    while(j <= r) w[k++] = q[j++];

    // 将辅助数组的值 覆盖原数组
    for(i = l , j = 0 ; j < k ; i++ , j++)
        q[i] = w[j];
}