堆排序

本文将介绍数据结构堆，以及堆排序

堆

堆是一种完全二叉树，分为小根堆和大根堆；以大根堆为例：根≥儿子。
通常堆是通过一维数组来实现的。

堆的存储方式：顺序存储（因为要支持随机索引）

在数组起始下标为0的情况下：

如果根节点的编号是 x 的话，它的左儿子编号是 2x + 1，右儿子编号是 2x + 2。

一个子节点是 p 的话，它的父节点是 ⌊ (p - 1) / 2 ⌋。

在数组起始下标为1的情况下：

如果根节点的编号是 x 的话，它的左儿子编号是 2x，右儿子编号是 2x + 1。

一个子节点是 p 的话，它的父节点是 ⌊ p / 2 ⌋。

在数组起始下标为1的情况下

大根堆的创建：

大根堆的删除（堆顶）：

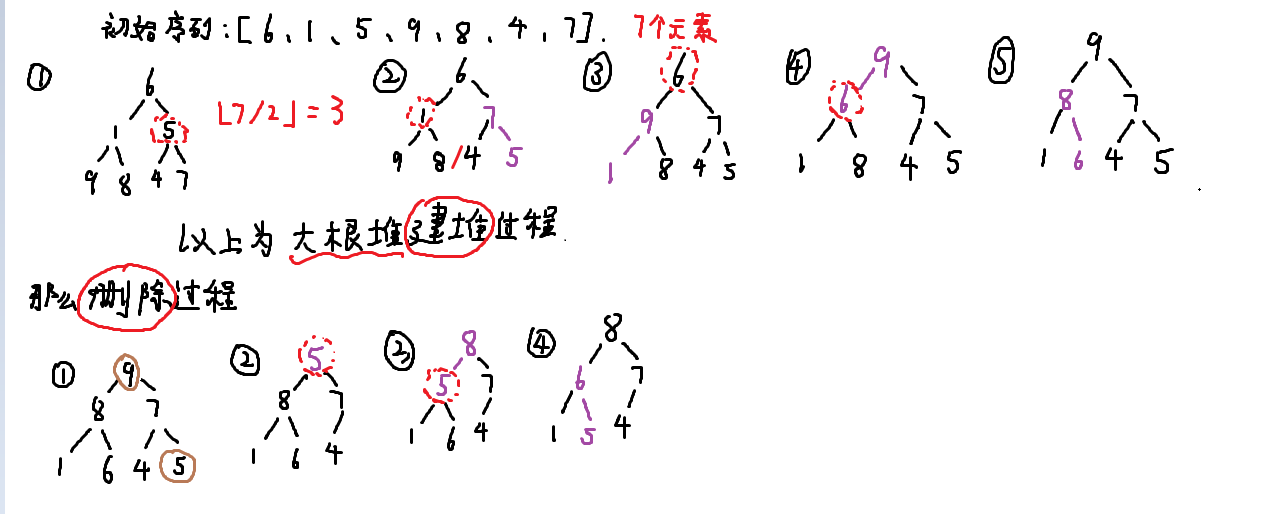
将堆的最后一个元素覆盖堆顶元素，堆的大小减1。（最后一个元素很好删）

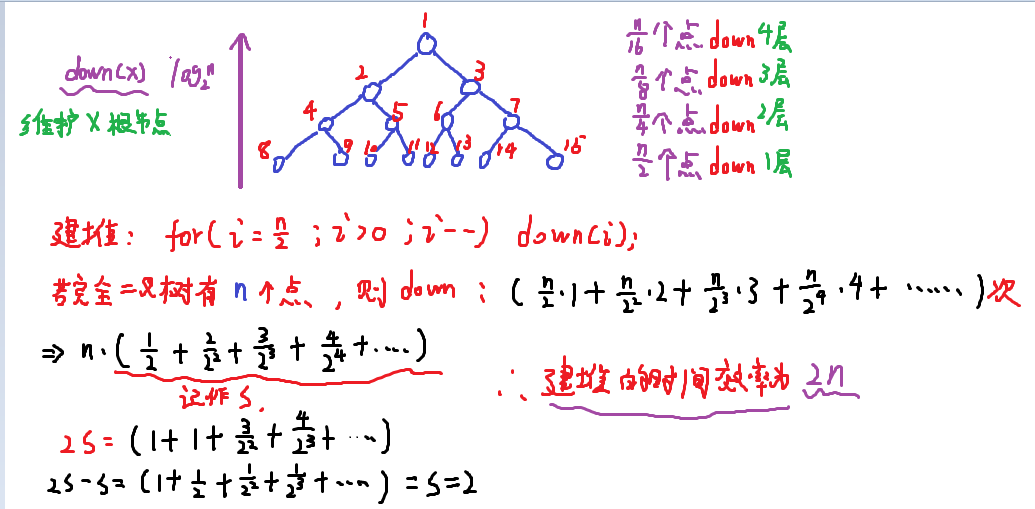
然后，从堆顶开始 down 一遍。

算法思想

使用大根堆，基于大根堆的操作基础；堆顶元素总是最大值，每次将堆顶元素与堆中最后一个元素互换，将堆的大小减1，然后 down(1)维护大根堆。反复如此，直到 n 个元素，执行 n - 1 次这样的操作，排序完成。

算法特性

时间复杂度：初始化建堆时间是O(n)，更改堆元素后重建堆时间是O(nlogn)，但一般认为全部情况都是O(nlogn)

空间复杂度：O(1)

稳定性：不稳定

算法模板

需要注意的是，需要维护一个变量 sz，它代表堆的容量

在数组起始下标为1的情况下：

// 维护以 u 为根的堆
void down(int u){
    int t = u;
    if(u * 2 <= sz && q[u * 2] > q[t]) t = u * 2;
    if(u * 2 + 1 <= sz && q[u * 2 + 1] > q[t]) t = u * 2 + 1;
    // 如果 t 和 u 不相等，说明有 儿子比父亲大，应该进行交换，然后进行维护之前儿子在的位置
    if(u != t){
        swap(q[t],q[u]);
        // 如果是上层发生改变，可能会牵涉到下层，因此需要递归down下去
        down(t);
    }
}

void heap_sort(){
    sz = n;
    // 从有分支的结点开始down
    for(int i = n / 2 ; i ; i--) down(i);

    // down完之后堆顶是最大的元素, 利用大根堆性质，进行n - 1次与数组最后一个元素交换可以进行排序
    for(int i = 0 ; i < n - 1 ; i++){
        swap(q[1],q[sz]);
        sz--;
        down(1);
    }
}