二维差分

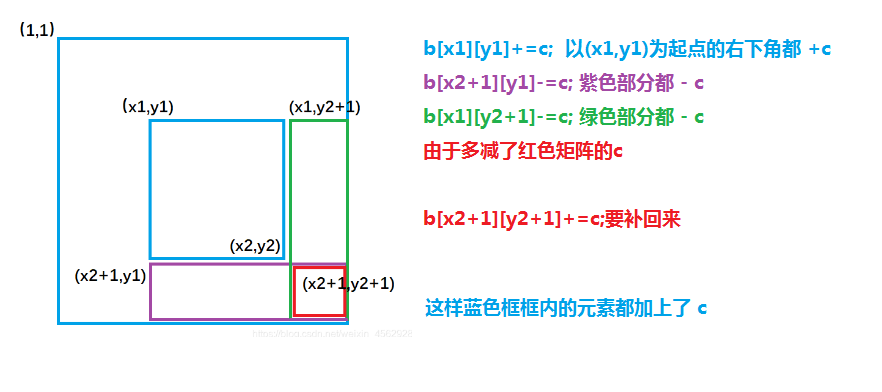
如果扩展到二维，我们需要让二维数组被选中的子矩阵中的每个元素的值加上c,是否也可以达到O(1)的时间复杂度。答案是可以的，考虑二维差分。
a[][]数组是b[][]数组的前缀和数组，那么b[][]是a[][]的差分数组

原数组： a[i][j]

我们去构造差分数组： b[i][j]

使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。

image-20230503232104902

798. 差分矩阵

输入一个 n 行 m 列的整数矩阵，再输入 q 个操作，每个操作包含五个整数 x1, y1, x2, y2, c，其中 (x1, y1) 和 (x2, y2) 表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上 c。

请你将进行完所有操作后的矩阵输出。

输入格式

第一行包含整数 n,m,q。

接下来 n 行，每行包含 m 个整数，表示整数矩阵。

接下来 q 行，每行包含 5 个整数 x1, y1, x2, y2, c，表示一个操作。

输出格式

共 n 行，每行 m 个整数，表示所有操作进行完毕后的最终矩阵。

数据范围

1 ≤ n,m ≤ 1000,
1 ≤ q ≤ 100000,
1 ≤ x1 ≤ x2 ≤ n,
1 ≤ y1 ≤ y2 ≤ m,
-1000 ≤ c ≤ 1000,
-1000 ≤ 矩阵内元素的值 ≤ 1000

输入样例：

1
2
3
4
5
6
7
3 4 3
1 2 2 1
3 2 2 1
1 1 1 1
1 1 2 2 1
1 3 2 3 2
3 1 3 4 1

输出样例：

1
2
3
2 3 4 1
4 3 4 1
2 2 2 2

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 1010;

int a[N][N], b[N][N];

int main(){
    
    int n, m, q;
    cin >> n >> m >> q;
    
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            cin >> a[i][j];
            
    // 求差分数组，类比一维数组求差分
    for(int i = 1; i <= n; i++)
        for(int j = 1; j <= m; j++)
            b[i][j] = a[i][j] - a[i - 1][j] - a[i][j - 1] + a[i - 1][j - 1];
            
    while(q --){
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        b[x1][y1] += c;
        b[x2 + 1][y1] -= c;
        b[x1][y2 + 1] -= c;
        b[x2 + 1][y2 + 1] += c;
    }
    
    // 求差分数组的前缀和，并且输出
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m; j++){
            b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1], cout << b[i][j] << " ";
        }
        cout << endl;
    }

    
    return 0;
}

感谢

林小鹿