差分应用场景

对区间内频繁地对数组中某个区间进行同一操作。例如将序列中[l, r]之间的每个数加上c这一操作，可能执行n次，每次的c不同，如果对原数组进行操作，每次操作都会花费O(n)的时间复杂度。如果使用该数组的差分数组进行操作，每次操作为O(1)。
然后求差分数组的前缀和即为所求结果。

差分数组

首先给定一个原数组a[]：a[1], a[2], a[3], … , a[n];

然后我们构造一个数组b[]： b[1] ,b[2] , b[3], … , b[i];

使得 a[i] = b[1] + b[2 ]+ b[3] +,..., + b[i]

也就是说，a数组是b数组的前缀和数组，反过来我们把b数组叫做a数组的差分数组。换句话说，每一个a[i]都是b数组中从头开始的一段区间和。

考虑如何构造差分b数组？

最为直接的方法

a[0]= 0;

b[1] = a[1] - a[0];

b[2] = a[2] - a[1];

b[3] = a [3] - a[2];

........

b[n] = a[n] - a[n-1];

差分数组的使用？

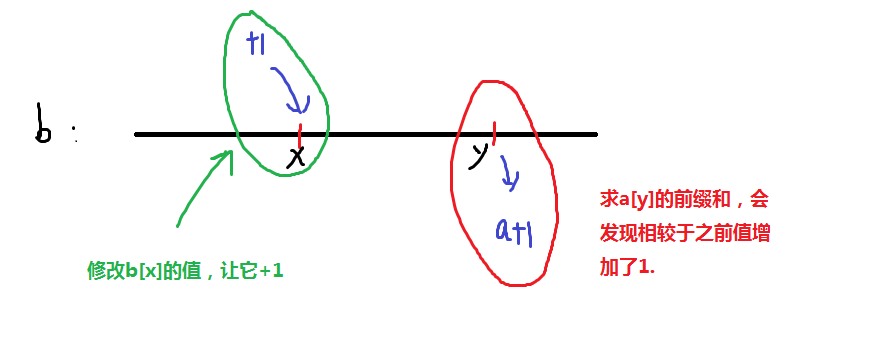
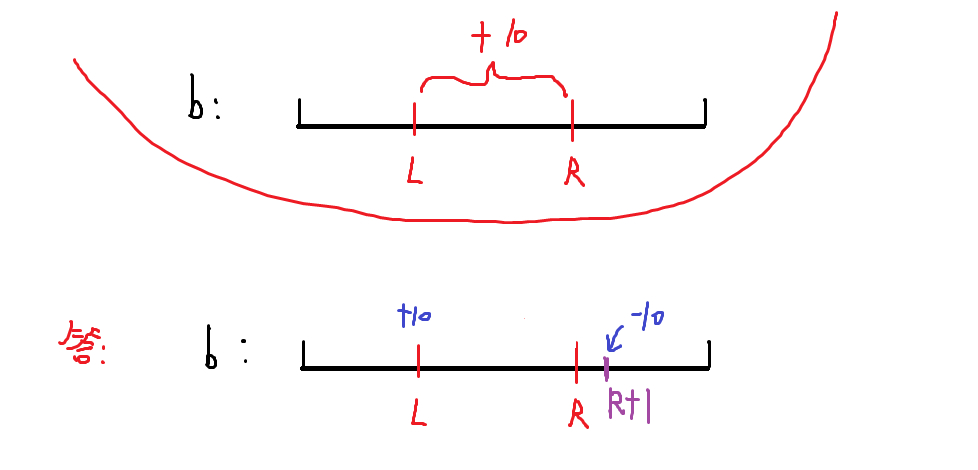
给定区间[l ,r ]，让我们把a数组中的[ l, r]区间中的每一个数都加上c。

由于a数组是b数组的前缀和，所以有这样的一个性质：

image-20230503215308523

抽象的来说：

image-20230503215648039

797. 差分

输入一个长度为 n 的整数序列。

接下来输入 m 个操作，每个操作包含三个整数 l, r, c，表示将序列中 [l, r] 之间的每个数加上 c。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 n 和 m。

第二行包含 n 个整数，表示整数序列。

接下来 m 行，每行包含三个整数 l，r，c，表示一个操作。

输出格式

共一行，包含 n 个整数，表示最终序列。

数据范围

1 ≤ n,m ≤ 100000,
1 ≤ l ≤ r ≤ n,
-1000 ≤ c ≤ 1000,
-1000 ≤ 整数序列中元素的值 ≤ 1000

输入样例：

1
2
3
4
5
6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

1
3 4 5 3 4 2

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 100010;

int a[N], b[N];

int main(){
    
    int n, m;
    cin >> n >> m;
    
    for(int i = 1; i <= n; i++) cin >> a[i];
    
    // 求差分数组
    for(int i = 1; i <= n; i++) b[i] = a[i] - a[i - 1];
    
    while(m --){
        int l, r, c;
        cin >> l >> r >> c;
        // 在[l, r]区间的元素都 + c
        b[l] += c;
        b[r + 1] -= c;
    }
    
    // 求一遍前缀和输出
    for(int i = 1; i <= n; i++) b[i] += b[i - 1], cout << b[i] << " ";
    
    cout << endl;
    
    return 0;
}

感谢

林小鹿