快速排序

本文将介绍王道书上的快排模板和一种不同于老教材的快排模板，图示是根据考研书上画的

算法思想

快速排序的核心操作为「哨兵划分」，其目标为：选取数组某个元素为基准数，将所有小于基准数的元素移动至其左边，大于基准数的元素移动至其右边。「哨兵划分」执行完毕后，原数组被划分成两个部分，即左子数组和右子数组，且满足左子数组任意元素＜基准数＜右子数组任意元素。因此，接下来我们只需要排序两个子数组即可，再将两个子数组执行「哨兵划分」……；直至子数组长度为1时终止递归。

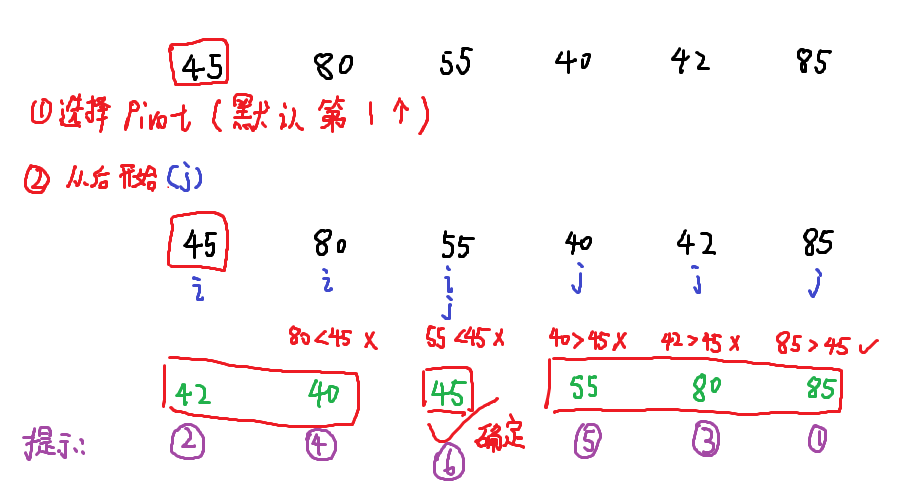
一个简单的例子：

以上是快速排序第一轮的模拟。

算法特性

时间复杂度：

快速排序的平均情况下的运行时间与其最佳情况下的运行时间很接近都是O(nlogn)
快速排序的运行时间与划分是否对称有关，快速排序的最坏情况发生在两个区域分别包含 n - 1 个元素和 0 个元素时，这种最大限度的不对称若发生在每层递归上，本应是二叉树的递归树退化成一叉树（单链表），即对应于初始排序表基本有序或基本逆序时，就得到最坏情况下的时间复杂度O(n²)。

空间复杂度：由于快速排序是递归的，需要借助一个递归工作栈

最好情况：O(logn) （二叉树）
平均情况：O(logn) （二叉树）
最坏情况：由于要进行 n - 1 次递归调用，所以栈的深度为O(n)

稳定性：不稳定

在快速排序算法中，每趟排序后会将枢轴（基准）元素放到其最终位置上。（考研写法）

快速排序为什么快？

从命名能够看出，快速排序在效率方面一定“有两把刷子”。快速排序的平均时间复杂度虽然与「归并排序」和「堆排序」一致，但实际 效率更高，这是因为：

出现最差情况的概率很低：虽然快速排序的最差时间复杂度为 O(n²) ，不如归并排序，但绝大部分情况下，快速排序可以达到 O(nlogn) 的复杂度。
缓存使用效率高：哨兵划分操作时，将整个子数组加载入缓存中，访问元素效率很高。而诸如「堆排序」需要跳跃式访问元素，因此不具有此特性。
复杂度的常数系数低：在提及的三种算法中，快速排序的比较、赋值、交换三种操作的总体数量最少（类似于「插入排序」快于「冒泡排序」的原因）。

算法模板1（背诵适合面试）

void quick_sort(int l , int r){
    // 区间大小为1，跳出循环
    if(l >= r) return;
    // 一开始 左边是 -1 右边是 length, pivot不取第一个元素是避免出现极端情况退化成单链表
    int i = l - 1 , j = r + 1 , pivot = q[(l + r) >> 1];
    while(i < j){
        do j--; while(q[j] > pivot);
        do i++; while(q[i] < pivot);
        if(i < j) swap(q[i],q[j]);
    }
    quick_sort(l,j);
    quick_sort(j+1,r);
}

算法模板2（考研版本）

int partition(int i, int j){
    int pivot = q[i];
    while(i < j){
        while(i < j && q[j] >= pivot) --j;
        q[i] = q[j];
        while(i < j && q[i] <= pivot) ++i;
        q[j] = q[i];
    }
    q[i] = pivot;
    return i;
}

void quick_sort(int l, int r){
    if(l < r){
        int pivot_pos = partition(l,r);
        quick_sort(l, pivot_pos - 1);
        quick_sort(pivot_pos + 1, r);
    }
}